迷宫问题是一个古老而经典的算法问题,自古以来就吸引了无数人的关注。在计算机科学领域,迷宫问题同样具有极高的研究价值。本文将以C程序为例,深入探讨迷宫问题的算法解析与应用,旨在为广大编程爱好者提供有益的参考。
一、迷宫问题概述

迷宫问题主要涉及以下三个要素:迷宫、起点和终点。迷宫通常由一系列相连的房间组成,起点和终点分别位于迷宫的某个房间内。求解迷宫问题的目标是在有限的时间内,找到从起点到终点的最佳路径。
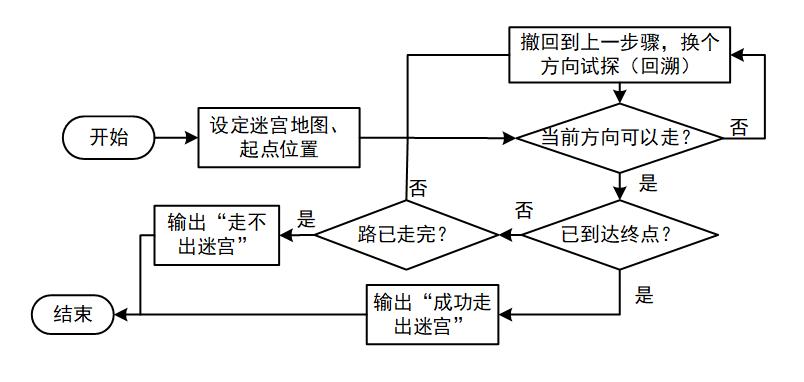
二、迷宫算法解析
1. 广度优先搜索(BFS)
广度优先搜索是一种经典的迷宫求解算法。它从起点开始,按照一定的顺序依次遍历迷宫中的房间,直到找到终点。BFS算法具有以下特点:
(1)易于实现:BFS算法相对简单,易于编程实现。
(2)易于理解:BFS算法的原理直观,易于理解。
(3)性能较好:BFS算法在大多数情况下具有较好的性能。
2. 深度优先搜索(DFS)
深度优先搜索是一种基于栈的迷宫求解算法。它从起点开始,沿着一条路径深入迷宫,直到无法继续前进,然后回溯到上一个房间,再尝试其他路径。DFS算法具有以下特点:
(1)易于实现:DFS算法相对简单,易于编程实现。
(2)适用于深度较大的迷宫:DFS算法在处理深度较大的迷宫时具有优势。
(3)性能一般:DFS算法在处理宽度较大的迷宫时,性能可能不如BFS算法。
3. A算法
A算法是一种启发式搜索算法,结合了BFS和DFS的优点。A算法通过估算从起点到终点的距离,优先选择最优路径。A算法具有以下特点:
(1)性能优异:A算法在大多数情况下具有较好的性能。
(2)适用于大型迷宫:A算法在处理大型迷宫时具有明显优势。
(3)计算量较大:A算法需要计算路径的估算距离,计算量相对较大。
三、迷宫算法的应用
迷宫算法在实际应用中具有广泛的应用前景。以下列举几个应用实例:
1. 游戏开发:迷宫算法在游戏开发中具有重要作用,如寻宝游戏、冒险游戏等。
2. 机器人路径规划:迷宫算法可用于机器人路径规划,帮助机器人避开障碍物,找到最佳路径。
3. 人工智能:迷宫算法在人工智能领域具有一定的研究价值,如机器学习、深度学习等。
迷宫问题是一个具有挑战性的算法问题,其算法解析与应用具有广泛的研究价值。本文以C程序为例,深入探讨了迷宫问题的三种算法:BFS、DFS和A算法。通过对这些算法的解析与应用,为广大编程爱好者提供了有益的参考。在未来的研究中,我们期待更多优秀的迷宫算法能够被提出,为相关领域的发展贡献力量。






