在计算机科学的世界里,回溯法(Backtracking)犹如一颗璀璨的明珠,闪耀着智慧的光芒。它是一种在解决问题的过程中,通过不断尝试和回退,直至找到最优解的算法思想。本文将深入探讨回溯法的原理、应用及其在解决复杂问题中的重要性。
一、回溯法的原理

回溯法的基本思想是从问题的解空间中,选择一个解分支进行探索,若此解分支不符合要求,则回溯到上一个状态,尝试其他解分支。这一过程不断重复,直至找到问题的解或所有可能的解。回溯法的核心在于递归,通过递归实现状态的回溯和分支的探索。
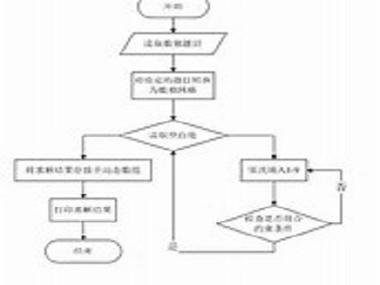
回溯法的主要步骤如下:
1. 确定问题的解空间:将问题分解为若干个状态,每个状态代表问题的一个可能解。
2. 选择一个解分支进行探索:从解空间中选择一个状态,尝试将其扩展为子状态。
3. 判断解分支是否满足条件:若解分支满足条件,则继续探索;若不满足条件,则回溯到上一个状态,尝试其他解分支。
4. 重复步骤2和3,直至找到问题的解或所有可能的解。
二、回溯法的应用
回溯法广泛应用于解决组合优化问题、图论问题、计算机科学中的算法设计等领域。以下列举几个典型的应用场景:
1. 八数码问题:通过回溯法寻找将初始状态变换为目标状态的最短路径。
2. 汉诺塔问题:利用回溯法求解将n个盘子从一柱移动到另一柱,且每次只能移动一个盘子的最优解。
3. 旅行商问题:利用回溯法寻找从起点出发,访问所有城市一次并返回起点的最短路径。
4. 图的着色问题:通过回溯法为无向图或有向图中的每个顶点分配颜色,使得相邻的顶点颜色不同。
三、回溯法的重要性
回溯法在解决复杂问题时具有重要意义,主要体现在以下几个方面:
1. 解决组合优化问题:回溯法可以有效地解决组合优化问题,如旅行商问题、背包问题等。
2. 探索问题的解空间:回溯法可以遍历问题的解空间,找到问题的所有可能解。
3. 提高算法效率:在解决某些问题时,回溯法可以优化算法的时间复杂度和空间复杂度。
4. 拓展算法设计思路:回溯法为算法设计提供了新的思路和方法,有助于开发新的算法。
回溯法作为一种重要的算法思想,在解决复杂问题中具有广泛的应用前景。随着计算机科学的发展,回溯法将继续发挥其独特的优势,为我国计算机科学事业的发展贡献力量。






