在数字的世界里,每个数字都拥有自己的性格,有的活泼,有的沉稳,有的热情,有的冷静。而在这其中,最为引人注目的便是奇偶性。奇偶性是数字世界的一种基本属性,它贯穿于数学的各个领域,影响着我们的生活。今天,就让我们一起来探索奇偶性的奥秘。
一、奇偶性的定义

奇偶性,顾名思义,是指一个数是奇数还是偶数的属性。在数学中,如果一个数能被2整除,则称它为偶数;反之,如果它不能被2整除,则称为奇数。例如,2、4、6、8等都是偶数,而1、3、5、7等都是奇数。
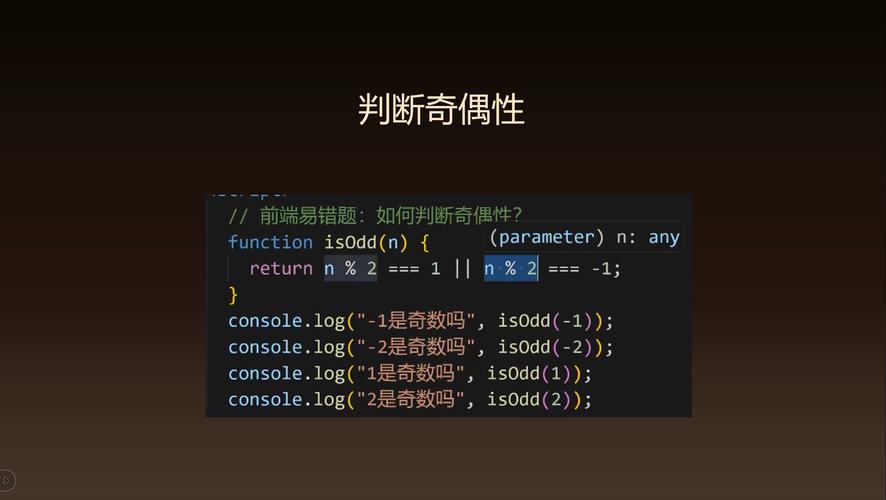
二、奇偶性在数学中的应用
1. 奇偶性在代数中的应用
在代数中,奇偶性是一个非常重要的概念。例如,在求解一元二次方程时,我们可以根据方程系数的奇偶性来判断方程的根的情况。当方程系数都是偶数时,方程的根一定是整数;当方程系数一个是奇数一个是偶数时,方程的根可能是整数也可能是分数。
2. 奇偶性在几何中的应用
在几何中,奇偶性同样具有重要的作用。例如,在研究平面图形的对称性时,我们可以利用奇偶性来判断图形的对称轴。当一个图形关于某条直线对称时,这条直线称为对称轴。如果对称轴两侧的图形关于y轴对称,那么这条对称轴就是y轴;如果对称轴两侧的图形关于x轴对称,那么这条对称轴就是x轴。
三、奇偶性在生活中的应用
1. 奇偶性在计算机科学中的应用
在计算机科学中,奇偶性被广泛应用于数据校验、数据加密等领域。例如,在数据传输过程中,我们可以通过计算数据的奇偶性来检测数据是否发生错误。如果数据发生错误,奇偶性检验将会发现。
2. 奇偶性在日常生活中的应用
在日常生活中,奇偶性也无处不在。例如,当我们挑选袜子时,如果左右两只袜子的颜色分别是奇数和偶数,那么它们就一定是一双。再比如,在玩扑克牌游戏时,奇偶性也可以帮助我们判断牌型。
四、奇偶性的哲学思考
从哲学的角度来看,奇偶性反映了数字世界的对立统一。在自然界中,我们经常看到“阴阳”这一概念,它也体现了对立统一的思想。奇数和偶数作为数字世界中的对立面,共同构成了这个世界的丰富多彩。
奇偶性作为数字世界的一种基本属性,贯穿于数学的各个领域,影响着我们的生活。通过对奇偶性的研究,我们可以更好地理解数字世界的规律,提升我们的思维能力。奇偶性也启示我们,在这个充满对立统一的世界里,我们要学会欣赏和接纳不同的存在,从而拥有更加丰富多彩的人生。















